 /
/ 
Time Limit: 3 sec / Memory Limit: 256 MB
配点 : 1600 点
問題文
joisinoお姉ちゃんは、長さ N の棒を持っています。 この棒には M 個の印がついています。 i 個目の印は、棒の左端から距離 X_i の位置についています。
joisinoお姉ちゃんは、この棒の上にいくつかの正方形を置くことにしました。 正方形を置くにあたって、以下のような条件があります。
- 辺の長さが整数の正方形しか置いてはならない。
- 全ての正方形は、底辺が棒と接するように置かなくてはならない。
- 正方形は、棒の上に敷き詰められている必要がある。 つまり、正方形が棒からはみ出したり、上に正方形が乗っていないような棒の部分が存在したりしてはならない。
- 棒の印がついている部分の真上は、2 つの正方形の境目であってはならない。
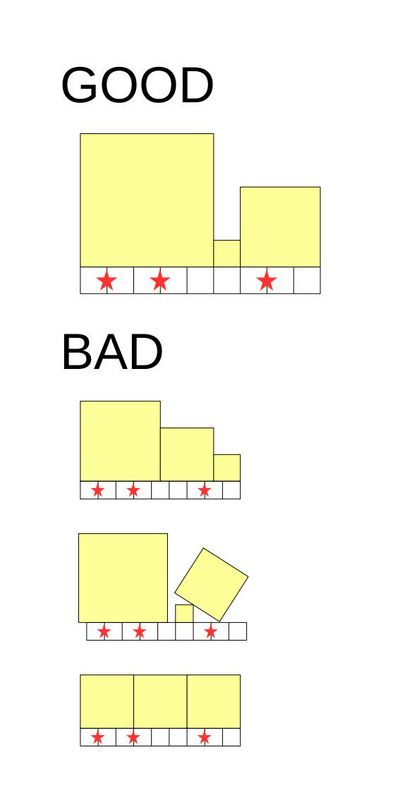
条件を満たす配置とそうでない配置の例
ある正方形の配置の美しさとは、置かれている正方形の面積をすべて掛け合わせた値です。 joisinoお姉ちゃんは、上の条件を満たすような正方形の配置全てについて、その美しさを求め、その総和を知りたくなりました。 あなたの仕事は、joisinoお姉ちゃんの代わりにこれを求めるプログラムを作ることです。 なお、答えは非常に大きくなることがあるので、10^9+7 で割った余りを出力してください。
制約
- 入力は全て整数である
- 1 \leq N \leq 10^9
- 0 \leq M \leq 10^5
- 1 \leq X_1 < X_2 < ... < X_{M-1} < X_M \leq N-1
入力
入力は以下の形式で標準入力から与えられる。
N M
X_1 X_2 ... X_{M-1} X_M
出力
あり得る正方形の配置全てについて、その美しさを求め、その総和を 10^9+7 で割った余りを出力せよ。
入力例 1
3 1 2
出力例 1
13
可能な配置は、
- 一辺の長さ 1 の正方形を左に、一辺の長さ 2 の正方形を右に置く
- 一辺の長さ 3 の正方形を置く
の 2 通りで、その美しさの合計は、(1 \times 1 \times 2 \times 2) + (3 \times 3) = 13 となります。
入力例 2
5 2 2 3
出力例 2
66
入力例 3
10 9 1 2 3 4 5 6 7 8 9
出力例 3
100
入力例 4
1000000000 0
出力例 4
693316425
Score : 1600 points
Problem Statement
Joisino has a bar of length N, which has M marks on it. The distance from the left end of the bar to the i-th mark is X_i.
She will place several squares on this bar. Here, the following conditions must be met:
- Only squares with integral length sides can be placed.
- Each square must be placed so that its bottom side touches the bar.
- The bar must be completely covered by squares. That is, no square may stick out of the bar, and no part of the bar may be left uncovered.
- The boundary line of two squares may not be directly above a mark.

Examples of arrangements that satisfy/violate the conditions
The beauty of an arrangement of squares is defined as the product of the areas of all the squares placed. Joisino is interested in the sum of the beauty over all possible arrangements that satisfy the conditions. Write a program to find it. Since it can be extremely large, print the sum modulo 10^9+7.
Constraints
- All input values are integers.
- 1 \leq N \leq 10^9
- 0 \leq M \leq 10^5
- 1 \leq X_1 < X_2 < ... < X_{M-1} < X_M \leq N-1
Input
Input is given from Standard Input in the following format:
N M
X_1 X_2 ... X_{M-1} X_M
Output
Print the sum of the beauty over all possible arrangements that satisfy the conditions, modulo 10^9+7.
Sample Input 1
3 1 2
Sample Output 1
13
There are two possible arrangements:
- Place a square of side length 1 to the left, and place another square of side length 2 to the right
- Place a square of side length 3
The sum of the beauty of these arrangements is (1 \times 1 \times 2 \times 2) + (3 \times 3) = 13.
Sample Input 2
5 2 2 3
Sample Output 2
66
Sample Input 3
10 9 1 2 3 4 5 6 7 8 9
Sample Output 3
100
Sample Input 4
1000000000 0
Sample Output 4
693316425